【第8回】データ分析の基本2(Step4~5: 課題解決の鍵を見出す)
- M.N.
- 2020-02-05
※ 『企業と人材』誌(産労総合研究所発行)に、2019年7月号から2020年6月号までの予定で『人材開発部門のデータ活用』を連載しています。誌面だと小さくなる図表を改めて掲載する他、誌面には掲載しきれない参考文献や参考情報を当ウェブサイトにて紹介します(毎月5日の発行日に合わせて公開)。連載本文PDF
【図1】 問題(部門固有の問題)の分析
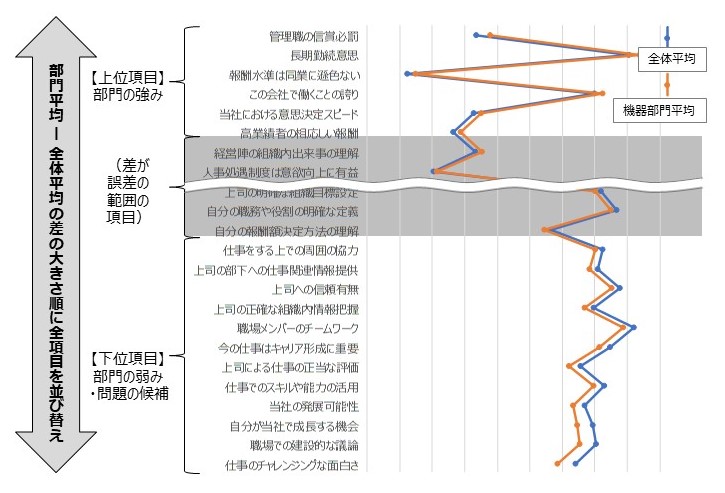
【図2】 課題解決・目的達成への要因の分析
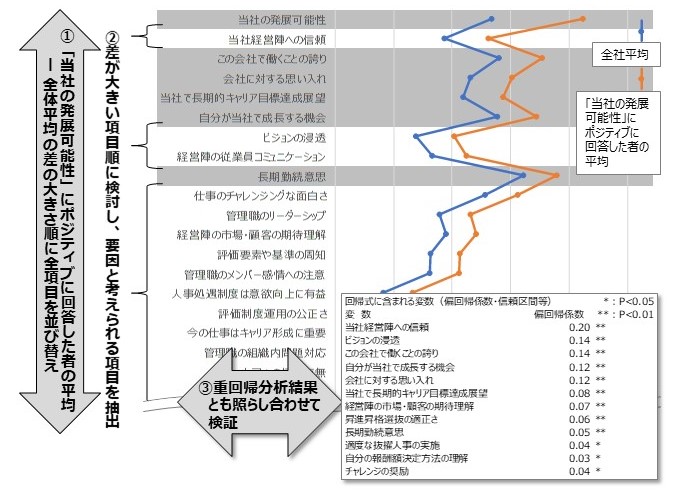
【差の大きさの検討を助けるソート、着色、折れ線グラフ】
差の大きさを比較検討する作業の実際としては、属性別に集計した設問項目別平均値を大きな一表に整理した上で、「平均値自体」および「平均値の差」の大小にもとづいて様々に設問項目をソートしながら、問題とその要因の候補を洗い出し、絞り込んでゆくことになります。その基本動作は集計表の並び替え(ソート)ですが、まずそもそも「値の高低を見えやすく」することも重要です。Excelの条件付書式機能を用いて数字の高低に応じて数表のセルに色をつけて「ヒートマップ」化する方法や、グラフ化する方法があります。
グラフの種類としては、ほとんどの場合「折れ線グラフ」が最適です。折れ線グラフは棒グラフや円グラフやレーダーチャートの要素を含み、かつ、複数の属性別集計を複数の線として同時に掲載でき、かつ「定規を当てながら」の精査にも適しています。折れ線グラフは「見た目の線が細い」ため、見た目のインパクトを重視する場合には、他のグラフ形式の方が適している場合もありますが、常に一定のグラフ形式でデータを示すことは、そのグラフ形式を組織の共通言語とすることにもつながり、データ分析結果の安定した理解と受け入れにつながります。それに向けて、グラフのテンプレートを作成しておき、データを入れ替えながら同じ形式でグラフを出力できるようにしておくことも一つの方法です。
【平均値での比較か、偏差値での比較か】
比較対象(全体平均や、目的変数とする設問項目の回答がポジティブな集団など)との差の大きさを、設問項目間で比較するにあたっては、理想的には、平均値そのままの差を比較するよりも、全回答中の偏差値の差を比較した方が望ましいと言えます。平均値そのままの差は、回答のバラツキが大きい設問項目の方が、差も大きくなりがちになるためです。偏差値では、回答のバラツキを事前に揃えることになるためその問題はありません。
ただし、プレゼン時の説明が複雑になることも考慮すると、通常は無理に偏差値で行う必要はないでしょう。設問項目間で回答値のバラツキの大きさが極端に違わないよう、設問項目を設計する際に設問文言に注意し、また回答データが得られた段階で実際の回答のバラツキ度合いをチェックしておく程度で十分です。
なお、偏差値による検討を行う場合には、あとから平均値を偏差値にするのではなく、集計に先立つ最初の段階で全ての回答値を偏差値化(標準化)してしまい、それを用いて平均値を計算することも一つの方法です。それにより、平均値を分析するのと同じ集計ツールを用いて、ただしインプットだけを変えることで、「偏差値版」の分析を行うことができます。
【差が誤差の範囲でないかのチェックと、有意差検定について】
「平均値のその差に意味があるのかどうかの判定(平均値の有意差の検定)」というテーマは、統計学の根幹を成すテーマとなっています。その大きな理由は、サイエンスが「測定値の背後にあると仮定される『真の値』は何か」ということを問題にすることにあると言ってよいと思います。
サイエンスならぬ人材開発における実用上の見地からは、「平均値のバラツキである『誤差』は元の回答データそのもののバラツキである『標準偏差』よりも小さく『標準偏差÷√N』程度になる」、ということさえしっかり頭の中に入っており、平均値の差を評価する時には「誤差の範囲でないかどうか」という議論ができれば十分である、というのが本連載の立場です。さらにできれば、「回答母数が少ない場合の誤差は標準誤差よりも若干大きめになるので注意すべし」といったことは意識しておくことがよいでしょう。
サイエンスの基礎科学としての統計学で用いられる判定方法はもっと複雑なもので、「平均値の分布は正規分布になることを中心極限定理に基づいて仮定し、一方、サンプル数が少ない場合の分布は真の分布と比べた歪みが大きくなるため、サンプル数に応じて正規分布を補正するカイ二乗分布およびそれに基づくt分布に基づいて信頼区間を設定し、帰無仮説に基づいて仮説検定を行う」というものです。この統計学固有の議論を前面に出す必要はありませんが、多くの統計手法において結果の妥当性を判断するためのロジックとして用いられるため、ロジックを理解しておくことは望ましいと言えます。(統計ソフトの出力結果には、このロジックに基づいて、「1%有意判定」を示す「**」や「5%有意判定」を示す「*」の印がつけられるのが一般的です。)第1回の参考文献の中で統計学の入門書として挙げた次の書籍では、その判定方法について、それが開発された経緯も含め、かなりわかりやすく解説されています。
西内啓 『統計学が最強の学問である[実践編]―データ分析のための思想と方法』
【そもそも何の誤差なのか】
誤差の範囲ということを言うためには、そもそも何の誤差なのか、ということを踏まえておく必要があります。誤差といっても、様々な種類があります。一般的に、アンケート形式の調査における誤差としては、「標本(サンプル)を抜き出したことによる標本誤差」が問題になります。「回答者は調査対象組織の全員ではないのだから、全員への全数調査を行った場合の結果とは乖離があるのではないか」というわけです。
もっとも本連載では、人材開発・組織開発プロセスとしての望ましさの見地から、社員意識調査の回答者はサンプリングすることなく全社員が回答に参加することを想定しています。多面評価の回答者も、被評価者の仕事ぶりを見ることができてフィードバックすべき人全員が回答に参加することを想定します。そうすると、たとえ若干の未回答者があったとしても、その調査は基本的に「全数調査」であって「標本(サンプル)調査」ではなく、従って「標本誤差」は問題にならないのではないか、という疑問も出てきます。
それについては、次のように考えます。調査票への回答とは(例えば3と回答しようか4と回答しようか迷った末に)たまたまその時にそのように(3または4と)回答したものにすぎず、すなわち偶然性が入り込んでいる、と考えます。一人の回答者の回答であっても、理想的には回答を何度も繰り返してもらってその平均値をとることでブレのない真の回答値に近づいていくもの、と考えます。実際、3と4の丁度中間くらいに真実がある、という場合には、何度も回答を繰り返す中で、平均値は3.5点に近づいていくことが想定できるでしょう。すなわち、回答の母集団は究極的には無限であり、たまたまの一回限りの回答値というサンプルを用いて、母集団の平均値を推定する、という考え方をとるのです。
一方、他の種類の誤差、たとえば「周囲に気を遣う人の常として回答が上振れしてしまいがちである」といった誤差(人間の計測器としての癖(バイアス)による測定誤差の一種)については、結果の解釈の段階で考慮することになります。
【相対評価も重要、かつ比較的正確であることについて】
本連載では、「設問項目別の集計値一つ一つを検討する」こともさることながら、「多数の設問項目を横並びで比較して序列化する」こと、すなわち項目間の相対評価も重視しています。
サイエンスとマネジメントでは統計手法に求められることも異なり、マネジメントでは相対評価がより重要になることは必然と言ってよいと思います。サイエンスのための統計学が、個別の現象の実証に目的があるのに対し、マネジメントのための統計学は、「認識能力の限界の中で最善の意思決定をしなければしなければならない」(いわゆる「限定合理性」と呼ばれる)制約の中でのより良い意思決定に目的があるためです。
そして連載本文でも述べているように、回答者による評価の甘辛のブレが大きく評価点の絶対値の信頼性が高くない場合であっても、「どの項目が相対的に強いか/弱いか」という評価順位は比較的安定しており、従って、全項目の中で何が相対的に問題か、ということは比較的精度高く議論できるという有り難い現実があります。この点を重視すべきことが、サイエンスにおけるにおける統計学に対する、マネジメントにおける統計学の特徴になると考えています。
相対評価は比較的安定している・・・このことは経験的には言われることで、例えば、USJのV字回復の立役者として名高いマーケッターの森岡毅氏も、「未来に対する質問においては、消費者データの絶対値は怪しいですが、相対での順位は比較的正しい」と、第3回の参考文献として挙げた書籍の中で言っています。
なぜ相対評価は比較的安定するのか・・・次のような理由付けが考えられます。
- 10個の対象を順位づけるとしたら、10回の評価をしているのではなく、実は10個のうち任意の2個の組み合わせ(10×9)の回数の評価をしているからである。
- ある対象の評価結果を条件に、他の対象を評価することになるため、いわゆる「ベイズ推定」を行っていることになり、評価の精度が高まるからである。
かつて、多面評価における少人数回答のフィードバックにも十分に意味があることを実証するために、他者評価の回答人数を1人から最大30人まで増やしながら、自己評価と他者評価の(どの項目の評価が高い/低いという)パターンの一致度合いが変化するかどうかを見たところ、「回答人数を増やしたところでパターンの一致度合いは有意には変わらない」すなわち「項目間の相対的な位置づけは回答人数に関わらず安定している」ことが言えた、ということもあります。
しかし、以上のようなことを学問的に裏付けている文献は、どうも見当たりません。今後は「サイエンスのための統計学」に加えて「マネジメントのための統計学」も求められるように思います。
【本連載における重回帰分析の使い方について】
重回帰分析は、高度な統計分析手法(多変量解析手法)の中で最も広汎に使われる手法であり、多くの解説をWebや書籍の中に見出すことができますので、紙数の関係上、連載本文での説明は最小限にさせていただきました。ここでは、本稿における重回帰分析の使い方と参考文献について補足します。
重回帰分析はもともと、「目的変数」を「説明変数」によって予測する式を作成するものですが、本稿では、「人や組織の望ましい状態の実現につながる要因」を探し出すために用います。すなわち、「ハイパフォーマーかどうか」あるいは「エンゲージメントが高いかどうか」といったことを「目的変数」とし、全ての設問項目を「説明変数」とした重回帰式を作成し、重回帰式の係数(標準偏回帰係数)の大小を見ることで、設問項目ごとの影響力を評価するのです。
(ただし、設問項目が多い場合には、設問項目間が干渉し合うこと(いわゆる多重共線性)により、正しい結果が得られない可能性が高まるため、設問項目設計時に設問項目間で意味内容の重複があまりないようにしておくことが前提です。また、Step6で因子分析を行って導き出した「因子得点」を用いてあらためて重回帰分析を行い、結果を見比べて結果の妥当性を確かめることも望ましい習慣と言えます。)
この使い方においては、説明変数の数がかなり多くなります(設問項目が60問であれば60個)。また、係数の大小を見る際には、重回帰式の係数そのものである「偏回帰係数」よりも「標準偏回帰係数」を見る方がより正確になります。よって、Excel標準のアドイン分析ツールを用いても重回帰分析は実施できるものの、説明変数が15個までという制約があり、また、「標準偏回帰係数」が出力表示されないという制約もあるため、既に紹介したExcelアドイン統計ソフトを用いることが現実的です。
また、「この回答者はその後離職した人か」といった2値(1か0か)の変数を目的変数とする重回帰分析も行います。一般的には、目的変数が2値の変数の場合には「重回帰分析」よりも「ロジスティック回帰分析」が適しているとされます。確かに、目的達成確率の予測のために回帰分析を用いるのであれば、「モデルの当てはまり」を評価したり、予測結果が必ず1と0の間の数値(確率)に収まるようにしたりするために、ロジスティック回帰分析が適していると考えられます。しかし予測のためではなく、目的に影響する要因を探るだけのために分析を行うのであれば、重回帰分析を使うことでかまわないというのが本連載の考えです。
◆
さて、重回帰分析の実践を学ぶための参考書ですが、結局、今回も既にご紹介している西内啓氏の次の書籍が、重回帰分析についての実践的なガイダンスも含まれており、最も適しているように思います。特に、現実感を失わないまま、割切りがよく暗算でも計算可能な(すなわち読みながら自分で計算して確かめることができる)例題が具体的な理解を容易にしてくれます。
西内啓 『統計学が最強の学問である[実践編]―データ分析のための思想と方法』
重回帰分析が広汎に使われる手法であり、西内氏自身も頻繁に用いていることは、次の記述からも窺えます。
- >「政策・教育・経営・公衆衛生といったありとあらゆる分野の研究結果が、先ほどの図表と同様に、回帰係数とその信頼区間やp値といった(あるいはこの一部を述べる)形で記述されているのだ。」
- >「z検定やt検定、単回帰分析といった手法は基礎として理解しておくことは大事だが、こうした手法を使うことよりも、業務で説明変数の候補が大量にあるデータがあるのであれば、とりあえずすべての説明変数を重回帰分析にかけてp値が小さく回帰係数が大きいものを探索する、というやり方をとることが圧倒的に多い。」
そして実践的なガイダンスとして、落とし穴になりやすい「ダミー変数の使い方」「オーバーフィッティング」「マルチコ(多重共線性)」「交互作用項」「変数選択(クラスター分析との併用)」についてもしっかりと述べられています。
そして、次の書籍における、ダウンロード可能な例題ファイルを使っての演習も有益と思います。
西内啓 『1億人のための統計解析 エクセルを最強の武器にする』